If you are intersted in project files only find it here - Github Repo for the project.

The inspiration to embark on this project actually came from dull working environment. I had most of my works on brown field PV projects; however every brown field project was a green field project to me. And I wanted to have technical insight on how project was laid initially. That led me to do some modeling, scripting & finally implementing my models and comparing them with standard commercial softwares. However, final project implementation was done in MATLAB, to analyze the results. So in the end, I got to analyze how my models performed compared to existing software models. Also, the actual job was done at the same time. From models I meant weather estimation models, Clearness Index Kt estimation models. I have further improvements to make, where I will train ANN models to estimate weather and clearness index; constraint: availability of useful & large dataset to train.


How did I start my modeling ?

The planning of PV projects actually begin with sizing of PV panels, what panel size do you actually require ? Size here refers to area of individual panel and also its power rating. However the area of PV panel required is determined by power input to the panels which actually depends on insolation on that panel. Let me assume power input to the panel as Pin, size of panel as \(A m^2\) and insolation at the panel as Li. And lets assume Pout as power output from the panel. As the system is set up, we must never forget the Second Law of Thermodynamics which account for loss in the system. So let us introduce effeciency (\eta) as another variable. So we got a simple system with Li, Pout, Pin, \eta, A as variables. We can visualize the system as; Pout = Pin*eff, where \(Pin = Li*A\). We get \(Pout = Li*A*\eta\) which gives $$A = {Pout\over Li*eff}.$$ Area of panel required is indeed more if effeciency of panel (\eta) is low and insolation (Li) is low. So at this point I came to conclusion PV panel sizing actually depends on Pout requirement, effeciency and insolation.

Pout requirement is fixed according to customer demand, effeciency (\eta) is fixed for a PV panel of certain model but insolation Li is a quantity dependent on several other variables. Maybe we create a insolation function \(Li = f(\phi,wv,\beta,surface,etc)\) were \phi is latitude location of place, wv is he weather variable, \beta is the tilt angle of PV panel, surface is the nature of surface around the location, hill/plains etc. So insolation Li is something we need to model at the very beginning of the project.

Insolation Modeling

Insolation modeling is not an easy job, insolation depends on several factors: location \({\phi}\), weather conditions at the location (wv), time of the day(hour angle wsr), time of the year \({\delta}\), surface of the area in the location, tilt angle of the PV panel \({\beta}\). So rushing in to model the entire system taking all these variables together wont give expected result. We must use divide and conquer principle. First divide all the factors taken into consideration. Depending on our model's capacity, we can take several factors under consideration then check the dependence of insolation (Li) on individual factor and then model the system. It is a tough task. So, I referred several papers, some books and lectures to see if there are certain equations describing the relationship. Actually, the equation or the function modeling took leverage of solar geometry, earth centric view of the sun & local centric view of the sun. then a model was concluded. I can't model them in a text website here. The geometry requires several figures. But I can break the relationship and model the dependence. We take the simplest system i.e, system with no tilt, PV panel which is horizontal. This excludes the dependence of insolation on tilt angle \({\beta}\). The insolation on a horizontal PV panel is given by:

\(Li = L(sin(\delta)sin(\phi)+cos(\delta)cos(\phi)cos(wsr))\) where wsr is the hour angle describing time of the day.

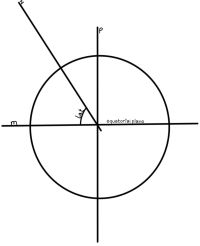
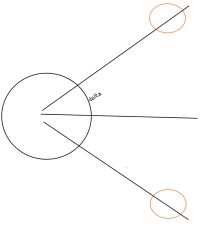
First picture shows dependence of insolation on latitude position of a place on earth with angle;lat, second picture shows how time of year; given by delta \({\delta}\) affects insolation (will talk later about it), and third picture shows how time of day from 6am to 6pm affects insolation

Insolation at a certain place on earth and its dependence on above mentioned factors are listed below:

  • Insolation & Latitude Position: For a person standing at a place on earth on a certain latitude position feels as if sun is directly above their head, from local centric point of view, insolation at that place is function of latitude location \({\phi}\).
  • Insolation and Time of Year: It is clear earth revolves around the sun which causes seasonal changes. The North hemisphere of earth is closest to sun during month of June, to be specific June 21 is cosidered summer solstice on Northern hemisphere, while on December, the northern hemisphere is farthest from the sun and to be specific Dec 21 is winter solstice for Northern hemisphere. It is as if the sun is moving from N to S hemisphere of the earth where sun has to cross equator to do so. In the second picture, this time of year for a certain place on earth is given by \({\delta}\).
  • Insolation and Time of Day:We clearly feel how insolation is affected by time of day. During morning and evening insolation is quite low while at noon it is at its peak. This time of day is reflected in insolation by angle wsr; also referred as sunrise angle.
  • and by the way, to be much clearer on this topic you must follow some lectures.

So we reach at the insolation as: \(Li = L(sin(\delta)sin(\phi)+cos(\delta)cos(\phi)cos(wsr))\)

Incident Energy on a Horizontal plane due to insolation Li

The insolation normal on a horizontal plane Li has the unit of \(kW/m2\); since \(Li*A\) gave us power input to the panel. To get incident enegy on horizontal PV panel, we must have the time factor. Energy is power consumed for a peroid of time till power is available so incident energy is total insolation for a certain period of time. That specific time is the total period of available insolation. So when we integrate insolation for the period time insolation is available; we get incident energy given by the insolation Li. The insolation available time for a day is given by the sunrise angles

Integrating insolation over the sunrise-sunset angles we get the incident energy. Given by
\(∫L(sin(\delta)sin(\phi))+cos(\delta)cos(\phi)cos(wsr))\) which gives incident energy on horizontal flat PV panel as $$Ho = {{24*L*sin(\delta)sin(\phi)+cos(\delta)cos(\phi)cos(wsr)}\over \pi}.$$
This gives us the incident energy on a horizontal plat PV taking latitude \({\phi}\) , time of year \({\delta}\) and hour angle wsr into consideration. The term L used here is the insolation previously denoted by Li. There are still few other things to consider. The insolation reaching at a place on earth must pass throgh the earth's atmosphere so insolation when taking earth's outer atmosphere into account is given by:
$$L = {Lsc*{[1+0.033*cos{360*N \over 365}]}}.$$ N here dontes day of the year. The term {1+(0.033*cos(360*N \over 365)} can simply be donted by k. So we get incident enery on a flat horizontal PV as:
$$Ho = {{24*k*Lsc*sin(\delta)sin(\phi)+cos(\delta)cos(\phi)cos(wsr)}\over \pi}.$$ The unit of measurement for incident energy is \(kWh/m^2\) per day.

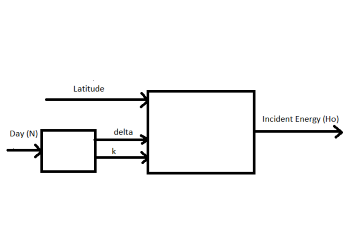
Given latitude location of the place, day of the year, we can easily model incident energy on horizontal plane at that specific location in that specific day.

We must now consider the tilt of the PV panel, keeping PV panel horizontal wont capture maximum incident energy throught the day, so tilt according to time of the day is required. One can also tilt the panel according to time of the year. PV panel can be tilted according to both time of the day and time of the year. Doing both requires complicated control and is expensive, so an optimal tilt angle for the panel throughout the year is determined and the panel is titled in that angle for that location.

I have a included a MATLAB script to find the optimum tilt angle for tha PV panel throughout the year here: optimalB The logic used here is pretty simple. I have defined a maximum tilt for the panel as Bmax = 30 degrees and Bmin = 0 degrees, then incident energy is calculated for each day of year varying tilt angle from Bmin to Bmax, that particular tilt angle whose minimum incident energy is the maximum compared to all tilt angles is taken as optimal tilt angle. It works because for that tilt angle; its minimum incident energy is greater compared to all others and we are guaranteed much greater incident energy.

However, one might want to change tilt angle to capture maximum incident energy at each day of the year, I have scripted another model for that too here: tiltaccordingly The model works fine and the logic here is incident energy is maximum at the location when suns declination angle (time of day) is exactly equal to latitude location of the place. So tilt required for that day is \({\beta}\) = Latitude location \({\phi}\) (in degrees) - Declination angle \({\delta}\) in degrees = 0. For any other day tilt is the difference of the two. So, one can track the sun each day for maximum incident energy. However, we have not yet considered atmospheric effects of the location.

We get incident energy on a tilted horizontal PV as: $$Hot = {{24*k*Lsc*sin(\delta)sin{(\phi-\beta)}+cos(\delta)cos{(\phi-\beta)}cos(wsr)}\over \pi}.$$

Incident Energy under Atmospheric Effect

Solar irradiance under atmospheric effect. Image-credit: Solar Spectrum

The figure depicts relationship between Spectral Irradiance and wavelength of the irradiation along with how spectral irradiance changes under atmospheric effect. Till now, the system was function of variables, viz. latitude location of place, hour angle, time of year given by declination angle. These three variables are of deterministic nature and can be exactly predicted. However, weather variable/atmospheric effect is a tricky one. The weather of a place is itslef dependent on several other probabilistic variables which cant be exaclty estimated, viz. air mass, humidity, cloud etc. The insolation vector from the sun is always attenuated by the atmoshperic effect and the attenuation not only depends on weather factors but also on the path length of the insolation vector. So, we can see in PV panels they are tested under standards of Air Mass (AM) = 1.5.

  • The Weather Model & Kt Model

    To accommodate the atmospheric effect/weather variable into our existing system we need a weather model. To start with a weather model, we must be very clear that we do not have a bechmark model that exactly estimates the weather conditions. We must narrow our weather models capacity such that it accurately predicts weather of our location but does not care much about other locations. Locaton here refers to our latitude location. Our latitude location must have a niche of its own. To start with a weather model, we only have historic weather data that are recorded, for now I am taking water content in the air as weather variable, I initially wanted to incorporate ANN based model to predict water vapor in the air; unfortunately for Nepal I could neither gather nor scrape any data on water vapor in the air. I eventually scraped data of India, however effective data was of less volume. I concluded ANN model wont capture the behavior with such data, so I had to work out something else here. Since weather is a seasonal phenomeneon or say it is periodic in nature, I thought we could instead model the weather as periodic function. So I took leverage of Fourier Series/ Fourier Curve fit Model, similar technique I applied when modeling moisture in the soil (thanks to my advisor MPP). Now we have some historic data on weather, maybe we store it in Wo. Wo holds weather data for certain latitude locations, for Nth day of the year. Now we need a model that predicts the data stored by Wo. Lets name it We. The periodic nature of weather is thus modeled as: $$We = {A1 + A2*sin(\tau) + A3*sin(2\tau) + A4*sin(3\tau) + A5*cos(\tau) + A6*cos(2\tau) + A7*cos(3\tau)}.$$ We go with the Occams Razor principle, i.e, we want to predict with certain accuracy, at the same time we do not want to complicate the system. So we go with only third order harmonics for sin and cosine. Weather estimation model is a function of \({\tau}\) which incorporates day of the year. And the coeffecients A1, A2 to A7 which can be kept under Ai are also functions of latitude location of the place given by "x" here. So this fourier coeffecients Ai can be modeled as: $$Ai = {ai1 + ai2*x + ai3*x^2}.$$ We have weather estimation model We as a function of day of the year/time & location of the place. Thus we can now estimate weather at certain place on certain time of the year. The known variables for this weather model are \({\tau}\) given by day of year and "x" given by locaton of place. We do not know the coeffecients Ai because we do not have ai1 to ai3. To know these coeffecints we must employ our recorded data of weather Wo. For modeling an accurate system we want our model to predict weather with least error. So, we implement least square error principle: \(Error = (We-Wi)^2\). To get coeffecients that predict weather accurately, the Error change with respect to coeffecients must be zero. So on doing so we get set of equations. Solving those equations will lead to coeffecients. I have scripted a MATLAB file for that here: Weather



    To model Kt also referred in our system as Clearness Index; we have similar procedure as mentioned for weather model. Kt is given by: $$Kt = {Ha \over Ho}.$$ Ha is measured using pyranometer and Ho can be calculated from above given formula for given location and time of year. Recorded data for Kt is now available. Estimated Ke for our location can be similarly estimated as weather was estimated using curve fitting method. We use $$Ke = {C1 + C2*sin(\tau) + C3*sin(2\tau) + C4*sin(3\tau) + C5*cos(\tau) + C6*cos(2\tau) + C7*cos(3\tau)}.$$ And Ci can modeled as fucntion of location of place "x" and weather "w". We use our above modeled weather model to estimate w in this case. Ci is given as: $$Ci = {ci1 + ci2*x + ci3*x^2 + ci4*w +ci5*w^2}.$$ Thus Kte can easily be estimated. Using Least Square Error principle, we find most appropriate coeffecients Ci for our model. Thus we get Kte model for our system. In this fashion, Weather Model & Kte Model is obtained. I have linked the script to Kte model here: Kte model

  • Tilt Factor

    Earlier we calculated Ho as incident energy on horizontal PV panel with no tilt, and Hot as incident energy on tilted PV panel. The ratio of Hot and Ho is the tilt factor given by: $$Tf = {Hot \over Ho}.$$ We already have Kt as $$Kt = {Ha \over Ho}.$$ Tilt factor also can be defined as $$Tf = {Hat \over Ha}.$$ which gives tilt of PV panel under atmospheric effect. So we finally get \(Hat = Tf*Kt*Ho\). This gives us the incident energy estimation for a latitude location on earth under atmospheric effect. This almost consolidates the physical variability under single model. Having Hat, we can size our PV panel according to the minimum Hat given by Hatmin such that we are PV panel has guarantee of delivering energy corresponding to the minimum Hat. And this energy provided by Hatmin must be equal to our required load so on the worst day of insolation too we are guaranteed that our load is supplied required power by the PV panels. More on this in later project where I have designed a complete single power stage system of PV array for 50kW plant along with MPPT. This project can also be interfaced to the grid.